Formal Algorithms for Transformers
Key Methodological Innovations
that have led to the Deep Learning revolution
(besides data avalability and democratization of computational resources)
Most DL algorithms aim at learning a parametric function \(f_{\theta}\) that approximates a target function \(f\) from a set of input-output pairs \(\lbrace (x_i, y_i) \rbrace_{i=1}^N\). This problem is solved by finding parameters \(\theta\) that minimize a loss function \(L\) that measures the discrepancy between \(f_\theta\) and \(f\).
Key Methodological Innovations
that have led to the Deep Learning revolution
(besides data a democratization of computational resources)
Stochastic Gradient Descent (optimization)
Automatic Differentiation (optimization)
Architectures (architecture): MLP, CNN, RNN, Transformers (Attention)
Overview
Feynman’s quote: “What I cannot create, I do not understand.”
If he was alive: “What I cannot code, I do not understand.”
Goal: understand inner workings of transformers (trying to code them).
Will not talk about training (optimization and gradient computation), but about architecture.
[Code Pointer *: example.py]
What is a Transformer?
It is a parametric function approximator, \(f_{\theta}\), specifically designed to work with sequences represented as matrices.
\(\theta\) are the parameters of the function, that are learned from (lots) training data.
e.g GPT-3 has 175 billion parameters.
Notation
Vocabulary: \(V\), is a finite set identified with \([N_V] \equiv \lbrace 1, \dots, N_V\rbrace\).
Letters, words, most commonly subwords (tokens).
Sequence: \(\boldsymbol{x} \equiv x[1:l] = x[1] \dots x[N] \in V^*\)
\(\ell_{\text{max}}\): maximum length of a sequence.
Data
Data is assumed to be set of independent and identically distributed (i.i.d.) sequences.
e.g. a collection of independent articles
If length of sequence is greater than \(\ell_{\text{max}}\), then sequence is broken into smaller chunks.
Details about the data depend on the task.
Transformers Tasks - Sequence Modeling
\(\boldsymbol{x}_n \in V^*\) for \(n = 1, \dots, N_{\text{data}}\) be a dataset of sequences
Assumed to be and i.i.d. sample from a distribution \(P\) over \(V^*\)
Goal: Learn an estimator \(\widehat{P}\) of \(P(\boldsymbol{x})\).
Usually decomposed: \(\widehat{P} = \widehat{P}_{\theta}(x[1]) \cdot \widehat{P}_{\theta}(x[2] | x[1]) \cdot \dots \cdot \widehat{P}_{\theta}(x[\ell] | x[1:\ell-1])\)
Goal: learn distribution over single token given the preceding tokens.
e.g. language modeling
Transformers Tasks - Sequence-to-Sequence Prediction
\((\boldsymbol{x}_n, \boldsymbol{z}_n) \sim P\) with \(P\) a distribution over \(V^* \times V^*\).
Goal: Learn an estimator \(\widehat{P}\) of \(P(\boldsymbol{z} | \boldsymbol{x})\).
Also decomposed using the chain rule of probability.
e.g. machine translation
Transformers Tasks - Sequence Classification
\((\boldsymbol{x}_n, c_n) \sim P(\boldsymbol{x}, c)\) with \(c \in [N_C]\) a finite set of classes.
Goal is to learn conditional distribution \(P(c | \boldsymbol{x})\).
e.g. sentiment analysis.
Tokenization
Goal: learn a vector representation of the sequence, useful for downstream tasks.
A transformer will learn a vector representation of each token in each sequence.
First thing is to break each sequence into tokens (vocabulary elements).
Several tokenization strategies. Take this text as an example
León is the best city in Spain.
Tokenization - Character-level
Take \(V\) to be the set of characters (in a given alphabet).
In the previous example, the sequence would be:
[L, e, ó, n, , …]
- Manageable vocabulary but requires longer sequences.
Tokenization - Word-level
Take \(V\) to be the set of English words.
In the previous example, the sequence would be:
[León, is, the, best, city, in, Spain]
Requires very large vocabulary.
Cannot deal with new words at test time.
Tokenization - Subword-level
\(V\) is a set of subwords.
Most utilized tokenization strategy nowadays.
GPT-3 uses a tokenizer of 50,257 subwords.
Tokenization
Each vocabulary element is associated with a unique integer.
Five special tokens are added to the vocabulary:
<PAD>: padding token<BOS>: beginning of sequence token<EOS>: end of sequence token<UNK>: unknown token<MASK>: mask token
Tokenization
Piece of text is represented as sequence of integers preceded by
<BOS>and followed by<EOS>tokens.If the text is smaller than \(\ell_{\text{max}}\), it is padded with
<PAD>tokens.If the text is longer than \(\ell_{\text{max}}\), it is broken into smaller chunks.
We will use \(N=\ell_{\text{max}}\) for simplicity.
Tokenization - Word-level
[Code Pointer 1: main.ipynb]
Architectural Components
- Token Embedding
- Positional Embedding
- Transformer Block
- Output Layer
Token Embedding
First task is to convert each sequence into a matrix of token embeddings.
Token embeddings map vocabulary elements into column vectors in \(\mathbb{R}^{D}\).
Sequence of tokens are matrices of size \(D \times N\).
Embeddings can be fixed or learned. Parameters are \(\boldsymbol{W_e} \in \mathbb{R}^{D \times N_V}\).
Positional Embedding
Vector representation of a token’s position in a sequence.
Map positions to vectors in \(\mathbb{R}^{D}\).
Can be fixed or learned. Parameters are \(\boldsymbol{W_p} \in \mathbb{R}^{D \times N}\).
Final input to the Transformer Block
- For the n-th token in the sequence, the input to the transformer block is: \[ \boldsymbol{x}^{(0)}_n = \boldsymbol{W}_e[:, x[n]] + \boldsymbol{W}_p[:, n] \in \mathbb{R}^{D} \]
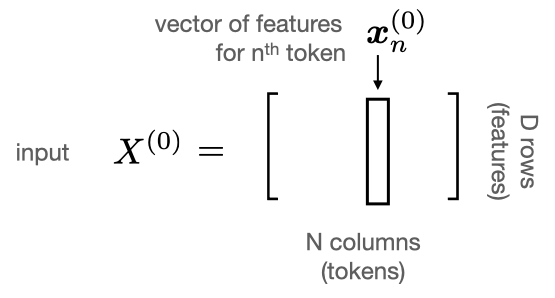
Final input to the Transformer Block
[Code Pointer 2: transformer.py]
Transformer Block
Each sequence corresponds to a matrix \(X^{(0)} \in \mathbb{R}^{D \times N}\).
Transformers generate a new representation of the input sequence by applying a series of transformer blocks.
\[ X^{(m)} = \text{TransformerBlock}(X^{(m-1)}) \]
Transformer Block
Block consists of two stages:
1. Self-Attention across the sequence: refines the representation of each token by considering the other tokens in the sequence: how much a word in position \(i\) depends on words in positions \(j\). [Vertically]
2. Multi-layer perceptron across features: refines the features representation of each token independently (without considering the other tokens in the sequence). [Horizontally]
1. Self-Attention across the sequence
Output of the self-attention mechanism is a matrix of size \(D \times N\), call it \(Y^{(m)}\). Output is produced aggregating information across the sequence for each feature using attention.
1. Self-Attention across the sequence
Attention
Specifically for the \(n\)-th location in the sequence, the output, denoted by \(\boldsymbol{y}^{(m)}_n\), is computed as a weighted average of the input features:
\[ \boldsymbol{y}^{(m)}_n = \sum_{n'=1}^{N} \boldsymbol{x}^{(m-1)}_{n'} \cdot A^{(m)}_{n'n} \]
\(A^{(m)}\) is the attention matrix of size \(N \times N\) whose elements are normalized over the columns so \(\sum_{n'=1}^{N} A^{(m)}_{n'n} = 1\).
1. Self-Attention across the sequence
Attention - Intuition
\(A^{(m)}_{n'n}\) will take high values for locations in the sequence \(n'\) that are relevant to the location \(n\).
For the whole sequence, we can write: \[ Y^{(m)} = X^{(m-1)} \cdot A^{(m)} \]
1. Self-Attention across the sequence
Attention - Intuition
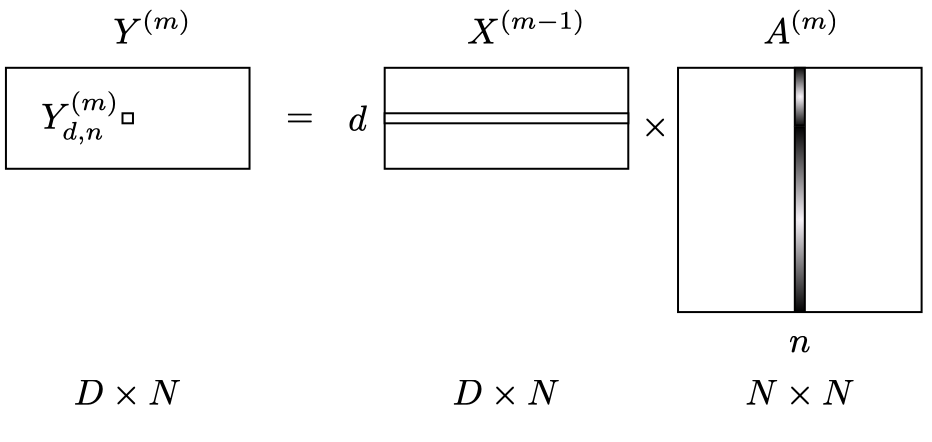
1. Self-Attention across the sequence
Self-Attention
What is the attention matrix \(A^{(m)}\)?
Attention matrix is generated from the sequence itself.
Idea
\[ A^{(m)} = \frac{\exp(\boldsymbol{x}_n^\top \boldsymbol{x}_{n'})}{\sum_{n''=1}^{N} \exp(\boldsymbol{x_n}^\top \boldsymbol{x_{n''}})} \]
1. Self-Attention across the sequence
Self-Attention
- An alternative
\[ A^{(m)} = \text{softmax}(\boldsymbol{x}_n^\top U^\top U \boldsymbol{x}_{n'}) \]
\(U\) projects features to a lower dimensional space, so is a \(K \times D\) matrix with \(K < D\).
Only some of the features of the input sequence need to be used to compute similarity.
1. Self-Attention across the sequence
Self-Attention
Numerator is symmetric in \(n\) and \(n'\)!!
Solution:
\[ A^{(m)} = \text{softmax}(\boldsymbol{x}_n^\top U_{\boldsymbol{k}}^\top U_{\boldsymbol{q}} \boldsymbol{x}_{n'}) \]
The quantity \(\boldsymbol{q}_n = U_{\boldsymbol{q}} \boldsymbol{x}_n\) is called the query vector.
The quantity \(\boldsymbol{k}_n = U_{\boldsymbol{k}} \boldsymbol{x}_n\) is called the key vector.
Matrices \(U_{\boldsymbol{q}} \in \mathbb{R}^{K \times D}\) and \(U_{\boldsymbol{k}} \in \mathbb{R}^{K \times D}\) are learned.
1. Self-Attention across the sequence
Multi-Head Self-Attention
- There is just one attention matrix \(A^{(m)}\). It would be useful for a pair of points to be similar across some dimensions and dissimilar across others.
1. Self-Attention across the sequence
Multi-Head Self-Attention
- Solution: compute multiple attention matrices.
\[ Y^{(m)} = \sum_{h=1}^{H} V_h^{(m)} X^{(m-1)} A_h^{(m)} \]
where
\[ A_h^{(m)} = \text{softmax} \left( (\boldsymbol{q}_{h,n}^{(m)}) \cdot (\boldsymbol{k}_{h,n'}^{(m)}) \right) \]
1. Self-Attention across the sequence
Multi-Head Self-Attention
- The dot product \(V_h^{(m)} X^{(m-1)}\) is called the value vector.
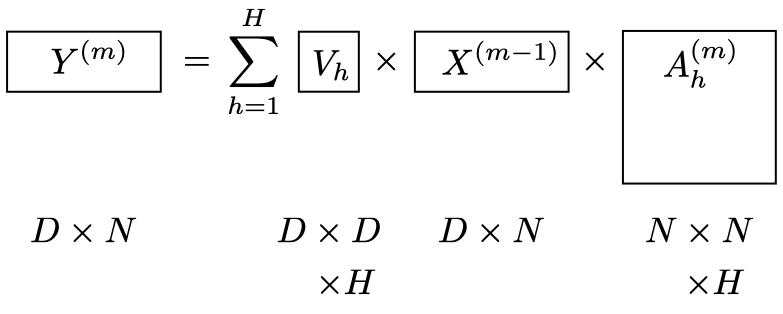
1. Self-Attention across the sequence
Multi-Head Self-Attention
Usually \(K=D/H\) in order to keep the number of parameters independent of the number of heads.
[Code Pointer 3: modules.py]
2. Multi-layer perceptron across features
This stage operates across the features, refining the representation using a non linear transformation.
2. Multi-layer perceptron across features
- We apply a multi-layer perceptron to the vector of features at each location \(n\) in the sequence independently.
\[ \boldsymbol{x}_n^{(m)} = \text{MLP}_\theta(\boldsymbol{y}_n^{(m)}) \]
Notice that the parameters of the MLP are the same for each location \(n\).
Transformer Block: all together
Rather than stacking MHSA and MLP directly, we use two transformations that produce more stable training: Residual Connection and Layer Normalization.
Transformer Block: all together
Residual Connection
Instead of directly specifying a function \(x^{(m)} = f_\theta(x^{(m-1)})\), the idea is to parameterize it as the identity function plus a residual term \(x^{(m)} = x^{(m-1)} + \text{res}_\theta(x^{(m-1)})\).
Modelling differences of representations rather than the representations themselves.
Works well when function being learned is close to the identity.
Stabilize learning.
Transformer Block: all together
Residual Connection
- Used after both the self-attention and the MLP with the idea that each applies a mild non-linear transformation.
Transformer Block: all together
Layer Normalization
Also stabilizes learning (helps with vanishing/exploding gradients).
Many choices, e.g. LayerNorm normalizes thre feature representation of each token independently.
\[ LayerNorm(X)_{d,n} = \frac{1}{\sqrt{\text{var}(\boldsymbol{x}_{n})}} (x_{d,n} - \text{mean}(\boldsymbol{x}_{n})) \gamma_d + \beta_d \]
- This prevents feature representations from blowing up in magnitude.
Transformer Block: all together
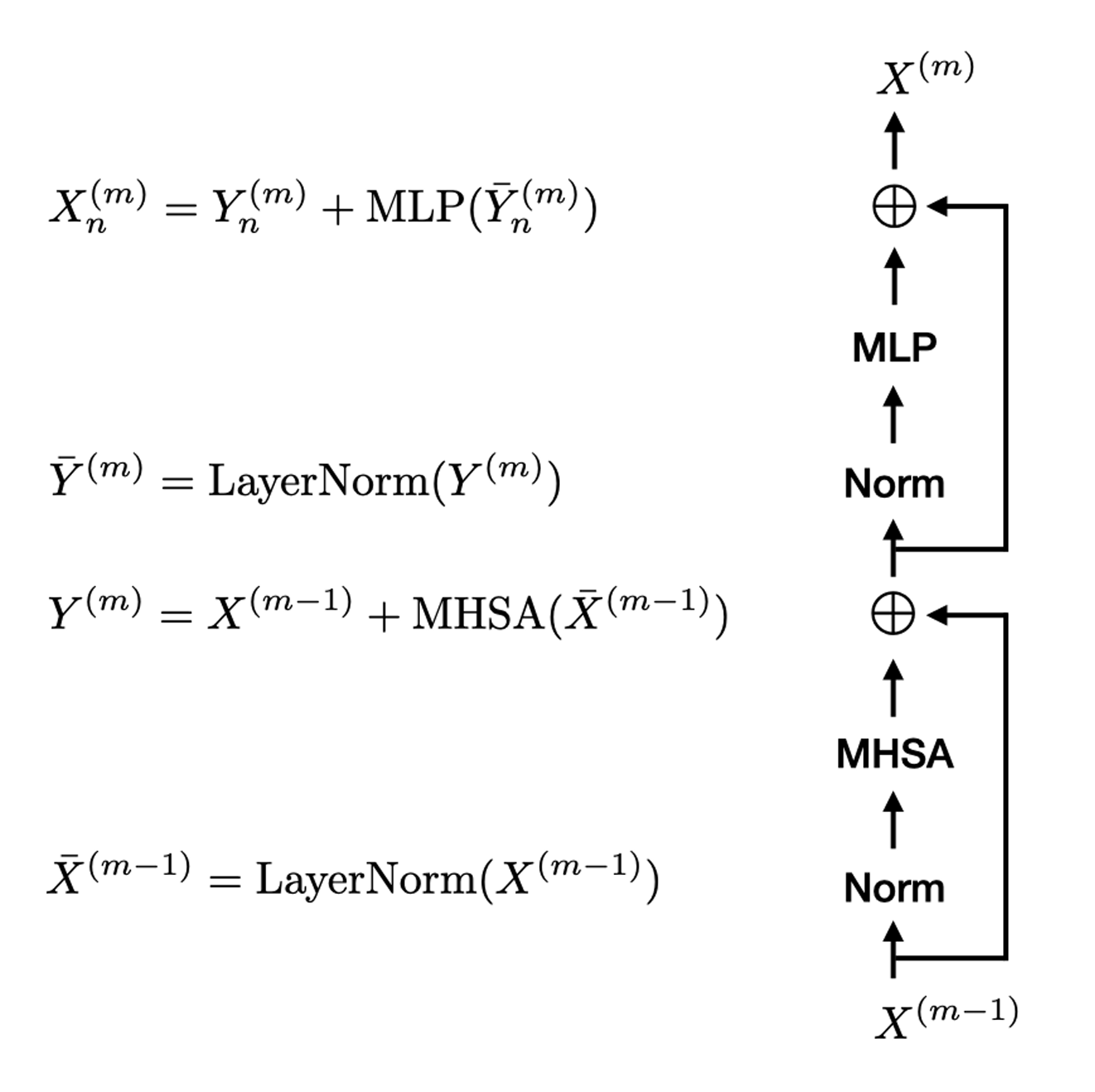
Transformer Block: all together
[Code Pointer 4: modules.py]
Output Layer
Depending on the task.
For example, for classification, we pass the transformer output \(X^{(M)}\) through a linear layer followed by a softmax over the classes. [Code Pointer 5: transformer.py]
In auto-regressive models, the goal is to predict the next token in the sequence given the previous ones: \(p(x[n] | x[1:n-1])\). For this, we need two modifications.
Tranformers - Auto-regressive models
Auto-regressive predictions is expensive: generating output for a sequence of length \(N\) requires \(N\) calls to the transformer.
We would like that if \(X^{(n)}\) is the output of the transformer for tokens \(x[1:n]\), and \(X^{(n+1)}\) is the output for tokens \(x[1:n+1]\), then \(X^{(n)} = X^{(n+1)}_{1:n}\).
But every token attends to all the other tokens in the sequence, so this is not the case.
Solution: mask attention matrix so it is upper triangular: \(A_{n'n} = 0\) for \(n' > n\). Then, representation of each token only depends on the previous tokens.
Tranformers - Auto-regressive models
We apply masked transformer blocks \(M\) times to the input sequence.
We take the representation at position \(n-1\) (\(\boldsymbol{x}_{n-1}^{(M)}\)) and pass it through a linear layer followed by a softmax to get the distribution over the next token.
\[ p(x[n] = w | x[1:n-1]) = p(x[n] | \boldsymbol{x}_{n-1}^{(M)}) = \frac{\exp \boldsymbol{g}_w^\top \boldsymbol{x}_{n-1}^{(M)}}{\sum_{w' \in V} \exp \boldsymbol{g}_{w'}^\top \boldsymbol{x}_{n-1}^{(M)}} \]
Loss Function and Training
[Code Pointer 6: main.ipynb]
The loss function depends on the task, but is usually based on the negative log-likelihood plus a regularization term.
Training is done using stochastic gradient descent or some of its variants such as Adam, RMSProp, etc.
This is done almost automatically using automatic differentiation in any deep learning framework, such as PyTorch or TensorFlow.
Thoughts - Equivariance
Without positional encoding, transformer representation of a sequence is permutation equivariant.
Equivariance to permutations is not always desirable. The solution is extremely simple: add positional embeddings to token embeddings (positional embeddings can be learned or fixed).
Thoughts - Transformers as GNNs
GNNs perform two types of operations: message passing, where each node receives messages from its neighbors and they are aggregated, and node update, where the node updates its representation based on the aggregated messages.
Transformers can be viewed as GNNs with a fully connected graph where each node attends to all the other nodes.
Sparse attention correspond to GNNs with a sparse connectivity graph.
Transformers can use different graphs at different layers!
Thoughts - Transformers Architectures
Several architectres:
Encoder-decoder, for sequence-to-sequence tasks.
Encoder-only, for learning useful representations that can be used for downstream tasks. (BERT).
Decoder-only, for text generation tasks (GPT).